Law of Conservation of Matter and Electron Configuration Review

In general, the law of conservation of momentum or principle of momentum conservation states that the momentum of an isolated system is a abiding. Periodic Table

Police of Conservation of Momentum

Newton's cradle. A device that demonstrates the Law of Conservation of Mechanical Energy and Momentum.

In general, the police force of conservation of momentum or principle of momentum conservation states that the momentum of an isolated organization is a abiding. The vector sum of the momenta (momentum is equal to the mass of an object multiplied past its velocity) of all the objects of a arrangement cannot exist inverse by interactions within the arrangement. In classical mechanics, this police force is unsaid by Newton'due south laws. This principle is a direct upshot of Newton's 3rd law.

Let us assume the 1 dimensional elastic collision of two billiard assurance,, the ball A and the ball B. Nosotros assume the net external force on this system of ii balls is null—that is, the merely meaning forces during the standoff are the forces that each ball exerts on the other. According to Newton's 3rd law, the two forces are always equal in magnitude and opposite in direction. Hence, the impulses that act on the two balls are equal and opposite, and the changes in momentum of the two balls are equal and contrary.

These two balls are moving with velocities v _A and five _B along the x centrality before the collision. After the collision, their velocities are 5' _A and five' _B . The conservation of the total momentum demands that the total momentum before the standoff is the same as the total momentum after the collision.

The police of conservation of linear momentum in words:

If no internet external strength acts on a arrangement of particles, the full linear momentum of the organization cannot change.

Conservation of Momentum and Energy in Collisions

The use of the conservation laws for momentum and energy is very of import also in particle collisions. This is a very powerful rule because it tin allow us to determine the results of a standoff without knowing the details of the collision. The law of conservation of momentum states that in the collision of two objects such as billiard balls, the total momentum is conserved. The assumption of conservation of momentum likewise equally the conservation of kinetic energy makes possible the adding of the concluding velocities in two-body collisions. At this betoken we have to distinguish between two types of collisions:

• Elastic collisions
• Inelastic collisions

Elastic Collisions

A perfectly elastic collision is defined every bit 1 in which in that location is no internet conversion of kinetic energy into other forms (such every bit heat or dissonance). For the cursory moment during which the 2 objects are in contact, some (or all) of the free energy is stored momentarily in the form of rubberband potential energy. Only if nosotros compare the total kinetic free energy just before the collision with the total kinetic energy just after the collision, and they are establish to be the aforementioned, then we say that the total kinetic free energy is conserved.

[xyz-ihs snippet="collisions"]

• Some large-calibration interactions like the slingshot type gravitational interactions (likewise known as a planetary swing-by or a gravity-aid manoeuvre) betwixt satellites and planets are perfectly rubberband.
• Collisions between very hard spheres may exist nigh elastic, so it is useful to calculate the limiting example of an elastic standoff.
• Collisions in ideal gases arroyo perfectly elastic collisions, equally practice scattering interactions of sub-atomic particles which are deflected past the electromagnetic force.
• Rutherford handful is the elastic scattering of charged particles also by the electromagnetic force.
• A neutron-nucleus scattering reaction may exist besides elastic, but in this case the neutron is deflected by the strong nuclear force.

Equations of Conservation of Momentum and Energy

Allow us assume the i dimensional elastic collision of 2 objects, the object A and the object B. These 2 objects are moving with velocities v_A and five_B along the x centrality earlier the collision. Later on the collision, their velocities are 5'_A and v'_B . The conservation of the total momentum demands that the total momentum before the collision is the same as the total momentum afterwards the standoff. Likewise, the conservation of the total kinetic energy, which demands that the total kinetic energy of both objects before the collision is the same as the total kinetic energy afterward the collision. Both law may exist expressed in equations as:

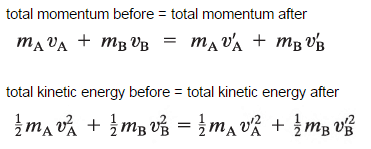
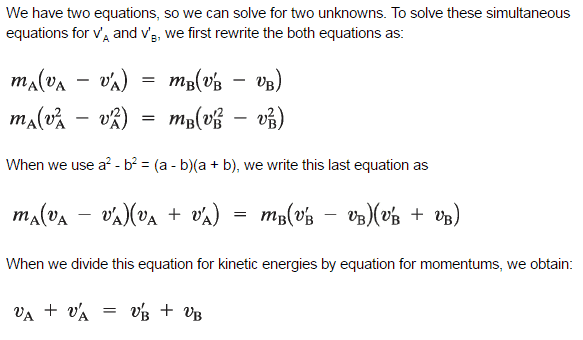
The relative speed of the ii objects afterwards the standoff has the same magnitude (but reverse direction) as before the collision, no matter what the masses are.

Inelastic Collisions

An inelastic collision is one in which part of the kinetic energy is changed to some other course of energy in the collision. Any macroscopic collision between objects will convert some of the kinetic energy into internal energy and other forms of energy, and then no large scale impacts are perfectly elastic. For example, in collisions of common bodies, such every bit two cars, some free energy is always transferred from kinetic energy to other forms of energy, such as thermal energy or energy of sound. The inelastic collision of two bodies e'er involves a loss in the kinetic energy of the arrangement. The greatest loss occurs if the bodies stick together, in which case the collision is chosen a completely inelastic collision. Thus, the kinetic energy of the system is non conserved, while the total free energy is conserved equally required by the general principle of conservation of energy. Momentum is conserved in inelastic collisions, but i cannot rail the kinetic energy through the standoff since some of information technology is converted to other forms of energy.

In nuclear physics, an inelastic collision is one in which the incoming particle causes the nucleus it strikes to get excited or to intermission up. Deep inelastic scattering is a method of probing the construction of subatomic particles in much the same mode as Rutherford probed the inside of the atom (see Rutherford scattering).

In nuclear reactors, inelastic collisions are of importance in neutron moderation process. An inelastic scattering plays an important role in slowing downwardly neutrons especially at high energies and past heavy nuclei. Inelastic scattering occurs to a higher place a threshold free energy. This threshold energy is college than the energy the beginning excited state of target nucleus (due to the laws of conservation) and it is given past post-obit formula:

E _t = ((A+1)/A)* ε _i

where E _t is known as the inelastic threshold energy and ε _one is the energy of the first excited state. Therefore especially handful information of ²³⁸ U, which is a major component of nuclear fuel in commercial power reactors, are one of the almost of import data in the neutron send calculations in the reactor core.

Example: Ballistic Pendulum

The ballistic pendulum is a kind of "transformer," exchanging the high speed of a light object (the bullet) for the low speed of a massive object.

A ballistic pendulum is a device for measuring the velocity of a projectile, such as a bullet. The ballistic pendulum is a kind of "transformer," exchanging the high speed of a low-cal object (the bullet) for the depression speed of a massive object (the block). When a bullet is fired into the block, its momentum is transferred to the block. The bullet's momentum can be determined from the aamplitude of the pendulum swing.

When the bullet is embedding itself in the block, it occurs and so quickly that the block does not move appreciably. The supporting strings remain almost vertical, then negligible external horizontal force acts on the bullet–block system, and the horizontal component of momentum is conserved. Mechanical free energy is not conserved during this stage, notwithstanding, because a nonconservative force does work (the force of friction betwixt bullet and block).

In the 2d phase, the bullet and block motion together. The only forces acting on this system are gravity (a conservative force) and the string tensions (which do no piece of work). Thus, as the block swings, mechanical energy is conserved. Momentum is not conserved during this stage, however, because there is a net external force (the forces of gravity and string tension don't cancel when the strings are inclined).

Equations governing the ballistic pendulum

In the kickoff stage momentum is conserved and therefore:

where v is the initial velocity of the projectile of mass g_P . v' is the velocity of the cake and embedded projectile (both of mass 1000_P + g_B ) just after the collision, earlier they accept moved significantly.

In the 2nd phase mechanical energy is conserved. We choose y = 0 when the pendulum hangs vertically, and and then y = h when the block and embedded projectile system reaches its maximum height. The system swings upwards and comes to remainder for an instant at a height y, where its kinetic energy is aught and the potential energy is (m_P + m_B)gh. Thus we write the law of conservation of free energy:

which is the initial velocity of the projectile and our last result.

When we use some realistic numbers:

• m_P = 5 g
• g_B = 2 kg
• h = 3 cm
• 5 = ?

then we accept:

Conservation Laws in Nuclear Reactions

A nuclear reaction is considered to exist the process in which ii nuclear particles (ii nuclei or a nucleus and a nucleon) interact to produce two or more nuclear particles or ˠ-rays (gamma rays). Thus, a nuclear reaction must crusade a transformation of at least one nuclide to another. Sometimes if a nucleus interacts with another nucleus or particle without changing the nature of whatsoever nuclide, the process is referred to a nuclear scattering, rather than a nuclear reaction.

In analyzing nuclear reactions, we apply the many conservation laws. Nuclear reactions are field of study to classical conservation laws for accuse, momentum, athwart momentum, and energy (including rest energies).  Additional conservation laws, not anticipated past classical physics, are are electric charge, lepton number and baryon number. Certain of these laws are obeyed under all circumstances, others are not. Nosotros have accustomed conservation of energy and momentum. In all the examples given we assume that the number of protons and the number of neutrons is separately conserved. Nosotros shall notice circumstances and conditions in which  this rule is not truthful. Where we are because non-relativistic nuclear reactions, it is essentially true. However, where nosotros are considering relativistic nuclear energies or those involving the weak interactions, we shall discover that these principles must be extended.

Some conservation principles have arisen from theoretical considerations, others are just empirical relationships. Notwithstanding, any reaction not expressly forbidden by the conservation laws will more often than not occur, if perchance at a deadening rate. This expectation is based on breakthrough mechanics. Unless the barrier between the initial and final states is infinitely high, there is e'er a non-zippo probability that a organization will make the transition between them.

For purposes of this commodity information technology is sufficient to annotation 4 of the key laws governing these reactions.

1. Conservation of nucleons. The full number of nucleons earlier and later a reaction are the same.
2. Conservation of charge. The sum of the charges on all the particles earlier and afterward a reaction are the same
3. Conservation of momentum. The total momentum of the interacting particles earlier and after a reaction are the aforementioned.
4. Conservation of energy. Energy, including remainder mass free energy, is conserved in nuclear reactions.

Types of Nuclear Reactions

Although the number of possiblenuclear reactions is enormous, nuclear reactions tin can be sorted by types. Most of nuclear reactions are accompanied by gamma emission. Some examples are:

• Rubberband scattering. Occurs, when no energy is transferred between the target nucleus and the incident particle.

 208Pb (n, n) 208Pb

•  Inelastic scattering. Occurs, when energy is transferred. The deviation of kinetic energies is saved in excited nuclide.

 40Ca (α, α') 40mCa

• Capture reactions. Both charged and neutral particles can be captured by nuclei. This is accompanied past the emission of ˠ-rays. Neutron capture reaction produces radioactive nuclides (induced radioactivity).

 238U (n, ˠ) 239U

• Transfer Reactions. The absorption of a particle accompanied by the emission of one or more particles is called the transfer reaction.

4He (α, p) 7Li

• Fission reactions. Nuclear fission is a nuclear reaction in which the nucleus of an atom splits into smaller parts (lighter nuclei). The fission procedure often produces free neutronsand photons (in the form of gamma rays), and releases a large amount of energy.

235U (n, 3 n)fission products

• Fusion reactions.  Occur when, two or more diminutive nuclei collide at a very loftier speed and join to class a new type of atomic nucleus.The fusion reaction of deuterium and tritium is particularly interesting because of its potential of providing free energy for the futurity.

3T (d, n) 4He

• Spallation reactions. Occur, when a nucleus is hit by a particle with sufficient energy and momentum to knock out several modest fragments or, smash it into many fragments.

• Nuclear decay (Radioactive decay). Occurs when an unstable cantlet loses energy by emitting ionizing radiation. Radioactive decay is a random process at the level of single atoms, in that, co-ordinate to breakthrough theory, it is impossible to predict when a particular atom will decay. There are many types of radioactive decay:
  • Blastoff radioactive decay. Alpha particles consist of two protons and two neutrons jump together into a particle identical to a helium nucleus. Because of its very large mass (more than 7000 times the mass of the beta particle) and its charge, it heavy ionizes material and has a very short range.

• Beta radioactivity. Beta particles are high-energy, high-speed electrons or positrons emitted by certain types of radioactive nuclei such as potassium-40. The beta particles have greater range of penetration than alpha particles, but still much less than gamma rays.The beta particles emitted are a class of ionizing radiation likewise known as beta rays. The product of beta particles is termed beta decay.

• Gamma radioactivity. Gamma rays are electromagnetic radiation of an very high frequency and are therefore high free energy photons. They are produced by the disuse of nuclei equally they transition from a loftier free energy state to a lower state known as gamma decay. Most of nuclear reactions are accompanied past gamma emission.

• Neutron emission.Neutron emission is a type of radioactive decay of nuclei containing excess neutrons (especially fission products), in which a neutron is simply ejected from the nucleus. This type of radiation plays central function in nuclear reactor control, because these neutrons are delayed  neutrons.

Conservation of Momentum in Nuclear Reactions – Neutron Moderation

See besides: Neutron Elastic Handful

See as well: Neutron Inelastic Scattering

See likewise: Neutron Moderators

It is known the fission neutrons are of importance in any chain-reacting organization. All neutrons produced by fission are born as fast neutrons with high kinetic energy. Before such neutrons tin efficiently cause boosted fissions, they must be slowed down past collisions with nuclei in the moderator of the reactor. The probability of the fission U-235 becomes very big at the thermal energies of dull neutrons. This fact implies increase of multiplication factor of the reactor (i.eastward. lower fuel enrichment is needed to sustain concatenation reaction).

The neutrons released during fission with an average free energy of two MeV in a reactor on average undergo a number of collisions (elastic or inelastic) earlier they are absorbed. During the scattering reaction, a fraction of the neutron'due south kinetic free energy is transferred to the nucleus. Using the laws of conservation of momentum and energy and the analogy of collisions of billiard balls for elastic scattering, it is possible to derive the following equation for the mass of target or moderator nucleus (Yard), free energy of incident neutron (E_i) and the energy of scattered neutron (E_s).

where A is the atomic mass number.In case of the hydrogen (A = i) equally the target nucleus, the incident neutron can exist completely stopped. Just this works when the direction of the neutron is completely reversed (i.due east. scattered at 180°). In reality, the direction of scattering ranges from 0 to 180 ° and the energy transferred too ranges from 0% to maximum. Therefore, the average energy of scattered neutron is taken as the average of energies with handful angle 0 and 180°.

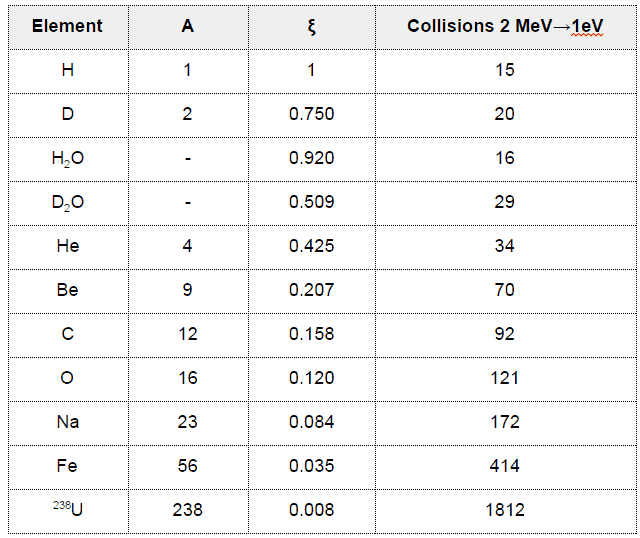
Moreover, it is useful to work with logarithmic quantities and therefore one defines the logarithmic energy decrement per collision (ξ) equally a key fabric abiding describing energy transfers during a neutron slowing down. ξ is non dependent on energy, only on A and is divers every bit follows: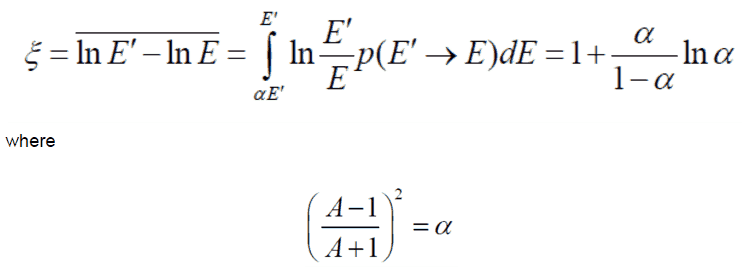For heavy target nuclei, ξ may be approximated past following formula: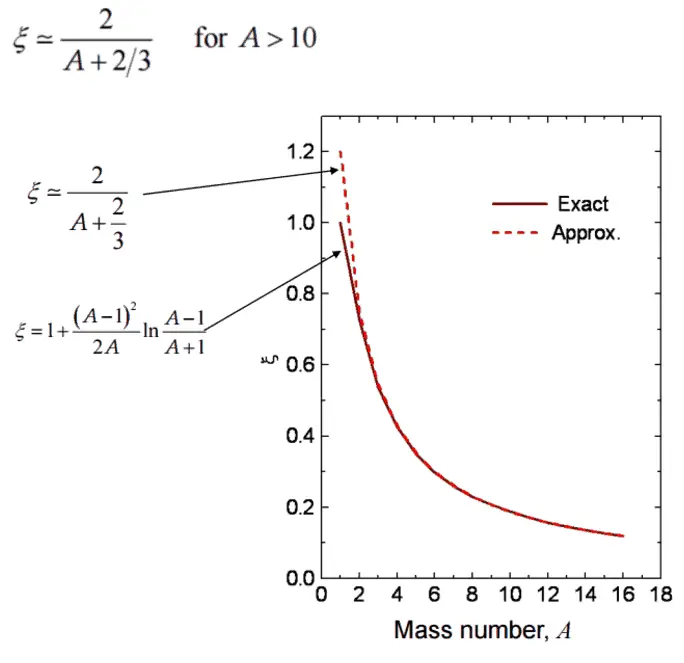From these equations information technology is easy to determine the number of collisions required to slow downwardly a neutron from, for example from two MeV to one eV.

Example: Make up one's mind the number of collisions required for thermalization for the ii MeV neutron in the carbon.

ξ_CARBON = 0.158

Northward(2MeV → 1eV) = ln two⋅x^{half dozen}/ξ =14.5/0.158 = 92

Tabular array of average logarithmic free energy decrement for some elements.

For a mixture of isotopes:

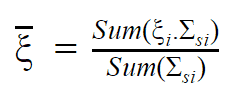
Case: Elastic Nuclear Collision

A neutron (n) of mass ane.01 u traveling with a speed of 3.60 ten ten^ivyard/s interacts with a carbon (C) nucleus (k_C = 12.00 u) initially at rest in an elastic caput-on collision.

What are the velocities of the neutron and carbon nucleus afterward the collision?

Solution:

This is an elastic head-on collision of 2 objects with unequal masses. Nosotros have to use the conservation laws of momentum and of kinetic free energy, and apply them to our system of two particles.

We can solve this system of equation or we can utilize the equation derived in previous section. This equation stated that the relative speed of the ii objects later on the collision has the same magnitude (simply opposite direction) every bit earlier the standoff, no matter what the masses are.

The minus sign for v' tells united states of america that the neutron scatters back of the carbon nucleus, because the carbon nucleus is significantly heavier. On the other hand its speed is less than its initial speed. This process is known as the neutron moderation and information technology significantly depends on the mass of moderator nuclei.

Momentum of a Photon

A photon, the quantum of electromagnetic radiation,  is an unproblematic particle, which is the strength carrier of the electromagnetic force. The modernistic photon concept was developed (1905) past Albert Einstein to explain of the photoelectric result, in which he proposed the beingness of discrete energy packets during the transmission of calorie-free.

In 1916, Einstein extended his concept of light quanta (photons) by proposing that a quantum of light has linear momentum. Although a photon is massless, it has momentum, which is related to its free energy E, frequency f, and wavelength past:

Thus, when a photon interacts with another object, energy and momentum are transferred, as if there were a collision betwixt the photon and matter in the classical sense.

Example: Momentum and Force of a Photon

Suppose the 10¹⁹ photons (let λ = 650 nm) emitted per second from the 100 Westward lightbulb.  Suppose all photons are focused onto a piece of black paper and captivated. Assume that the momentum of a photon changes from p = h/λ to aught.

Calculate the momentum of one photon and calculate the force all these photons could exert on the paper.

Solution:

We utilize the formula of momentum of a single photon:

Momentum of a Photon – Compton Scattering

In Compton scattering, the incident gamma-ray photon is deflected through an angle Θ with respect to its original direction. This deflection results in a decrease in energy (decrease in photon'south frequency) of the photon and is called the Compton effect.
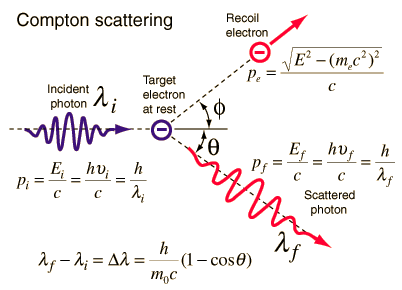
Source: hyperphysics.phy-astr.gsu.edu

The Compton formula was published in 1923 in the Concrete Review. Compton explained that the X-ray shift is caused by particle-like momentum of photons. Compton scattering formula is the mathematical human relationship between the shift in wavelength and the scattering angle of the Ten-rays. In the case of Compton scattering the photon of frequencyf collides with an electron at residuum. Upon collision, the photon bounces off electron, giving up some of its initial energy (given past Planck'south formula Eastward=hf), While the electron gains momentum (mass x velocity), thephoton cannot lower its velocity. Every bit a event of momentum conservation police force, the photon must lower its momentum given past:

So the decrease in photon's momentum must be translated intosubtract in frequency (increase in wavelength Δλ = λ' – λ). The shift of the wavelength increased with scattering angle according tothe Compton formula:

where λ is the initial wavelength of photon λ' is the wavelength after scattering, his the Planck constant = 6.626 10 x^-34 J.s, thousand_e  is the electron rest mass (0.511 MeV)c is the speed of lite Θ is the scattering bending. The minimum change in wavelength (λ′ −λ) for the photon occurs when Θ = 0° (cos(Θ)=ane) and is at to the lowest degree nix. The maximum change in wavelength (λ′ −λ) for the photon occurs when Θ = 180° (cos(Θ)=-1). In this example the photon transfers to the electron as much momentum as possible. The maximum modify in wavelength tin can exist derived from Compton formula:

The quantity h/thou_eastwardc is known as theCompton wavelength of the electron and is equal totwo.43×x⁻¹² m.

Conservation of Momentum in Fluid Dynamics

In general, the law of conservation of momentum or principle of momentum conservation states that the momentum of an isolated organisation is a abiding. The vector sum of the momenta (momentum is equal to the mass of an object multiplied by its velocity) of all the objects of a system cannot exist inverse past interactions within the organization. In classical mechanics, this law is unsaid by Newton'southward laws.

In fluid dynamics, the analysis of movement is performed in the same way as in solid mechanics – by employ of Newton's laws of movement. Every bit can be seen moving fluids are exerting forces. The elevator strength on an aircraft is exerted by the air moving over the fly.

A jet of water from a hose exerts a force on whatever it hits. Just here it is not clear what mass of moving fluid we should use and therefore it is necessary to use a dissimilar grade of the equation.

Newton's 2nd Constabulary can be written:

The rate of alter of momentum of a body is equal to the resultant force interim on the body, and takes place in the direction of the force.

We assume fluid to be both steady and incompressible. To decide the charge per unit of change of momentum for a fluid nosotros will consider a streamtube (control volume) every bit we did for the Bernoulli equation. In this command book any modify in momentum of the fluid within a control volume is due to the activity of external forces on the fluid within the volume.

As can be seen from the picture the control book method can be used to analyze the law of conservation of momentum in fluid. Command volume is an imaginary surface enclosing a volume of interest. The control volume tin exist fixed or moving, and it tin be rigid or deformable. In society to make up one's mind all forces interim on the surfaces of the command book nosotros take to solve the conservation laws in this control book.

The first conservation equation nosotros take to consider in the control volume is the continuity equation (the law of conservation of matter). In the simplest form it is represented by following equation:

∑ṁ_in = ∑ṁ_out

Sum of mass menstruum rates entering per unit of measurement fourth dimension = Sum of mass flow rates leaving per unit time

The 2nd conservation equation we have to consider in the control volume is the momentum formula.

Momentum Formula

In the simplest form the momentum formula tin be represented by following equation:

–

Choosing a Control Volume

A control book can be selected as any arbitrary volume through which fluid flows. This book can be static, moving, and even deforming during menstruum. In lodge to solve whatsoever trouble we have to solve basic conservation laws in this volume. It is very important to know all relative menstruation velocities to the control surface and therefore it is very important to define exactly the boundaries of the command book during an analysis.

Example: The force acting on a deflector elbow

An elbow (let say of main piping) is used to deflect water flow at a velocity of 17 thousand/southward. The piping diameter is equal to 700 mm. The gauge pressure within the pipe is about 16 MPa at the temperature of 290°C. Fluid is of constant density ⍴ ~ 720 kg/g³ (at 290°C). The angle of the elbow is 45°.

Summate the force on the wall of a deflector elbow (i.e. calculate vector F₃).

Assumptions:

• The flow is steady.
• The frictional losses are negligible.
• The weight of the elbow is negligible.
• The weight of the h2o in the elbow is negligible.

Nosotros take the elbow as the control volume. The command volume is shown at the picture. The momentum equation is a vector equation so it has three components. We take the 10- and z- coordinates every bit shown and we volition solve the problem separately co-ordinate to these coordinates.

First, let us consider the component in the x-coordinate. The conservation of linear momentum equation becomes:

2d, allow usa consider the component in the y-coordinate. The conservation of linear momentum equation becomes:

The last force acting on the wall of a deflector elbow volition exist:

Example: Water Jet Hitting a Stationary Plate

A stationary plate (eastward.g. blade of a watermill) is used to deflect water flow at a velocity of 1 m/southward and at an angle of 90°. It occurs at atmospheric pressure and the mass catamenia rate is equal to Q =1 m³/southward.

1. Calculate the pressure force.
2. Calculate the trunk force.
3. Summate the full force.
4. Summate the resultant force.

Solution

1. The pressure force is nil equally the force per unit area at both the inlet and the outlets to the control volume are atmospheric.
2. As the control book is small we can ignore the body forcefulness due to the weight of gravity.
3. F_x = ρ.Q.(w_1x – westward_2x) = 1000 . 1 . (1 – 0) = 1000 N
   F_y = 0
   F = (grand, 0)
4. The resultant force on the plane is the same magnitude simply in the opposite direction as the total forcefulness F (friction and weight are neglected).

The water jet exerts on the plate the strength of 1000 N in the ten-management.

References:

Nuclear and Reactor Physics:

1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Applied science, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
3. W. Chiliad. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
4. Glasstone, Sesonske. Nuclear Reactor Engineering science: Reactor Systems Applied science, Springer; 4th edition, 1994, ISBN: 978-0412985317
5. Westward.S.C. Williams. Nuclear and Particle Physics. Clarendon Printing; ane edition, 1991, ISBN: 978-0198520467
6. Kenneth Due south. Krane. Introductory Nuclear Physics, 3rd Edition, Wiley, 1987, ISBN: 978-0471805533
7. One thousand.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
8. Robert Reed Burn down, Introduction to Nuclear Reactor Operation, 1988.
9. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and ii. Jan 1993.

Advanced Reactor Physics:

1. One thousand. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-ii.
2. Yard. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Club, 1985, ISBN: 0-894-48029-4.
3. D. 50. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Guild, 1993, ISBN: 0-894-48453-2.
4. Eastward. East. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Social club, 1993, ISBN: 0-894-48452-4.

See also:

Laws of Conservation

Nosotros promise, this article, Law of Conservation of Momentum, helps yous. If so, give us a like in the sidebar. Master purpose of this website is to help the public to acquire some interesting and important information most radiations and dosimeters.

mccainranyth.blogspot.com

Source: https://www.periodic-table.org/what-is-law-of-conservation-of-momentum-definition/

Share this post